In che modo il concetto matematico di Crescita esponenziale ci può aiutare a comprendere come si svilupperà un’epidemia?
Riportiamo di seguito una sintesi del video Crescita esponenziale ed epidemie, realizzato dal Canale youtube 3Blue1Brown, specializzato in video divulgativi sui principali concetti matematici.
Per chi comprende bene l’inglese, il video integrale è riportato al link precedente, oppure in fondo a questa pagina.
Per chi ha qualche difficoltà con l’inglese, per facilitare la comprensione del video ricordiamo che su youtube è possibile attivare i sottotitoli in italiano.
Qual è il vero significato di crescita esponenziale?
Se giorno dopo giorno moltiplichiamo un numero per un fattore proporzionale al numero stesso, cosa accade?
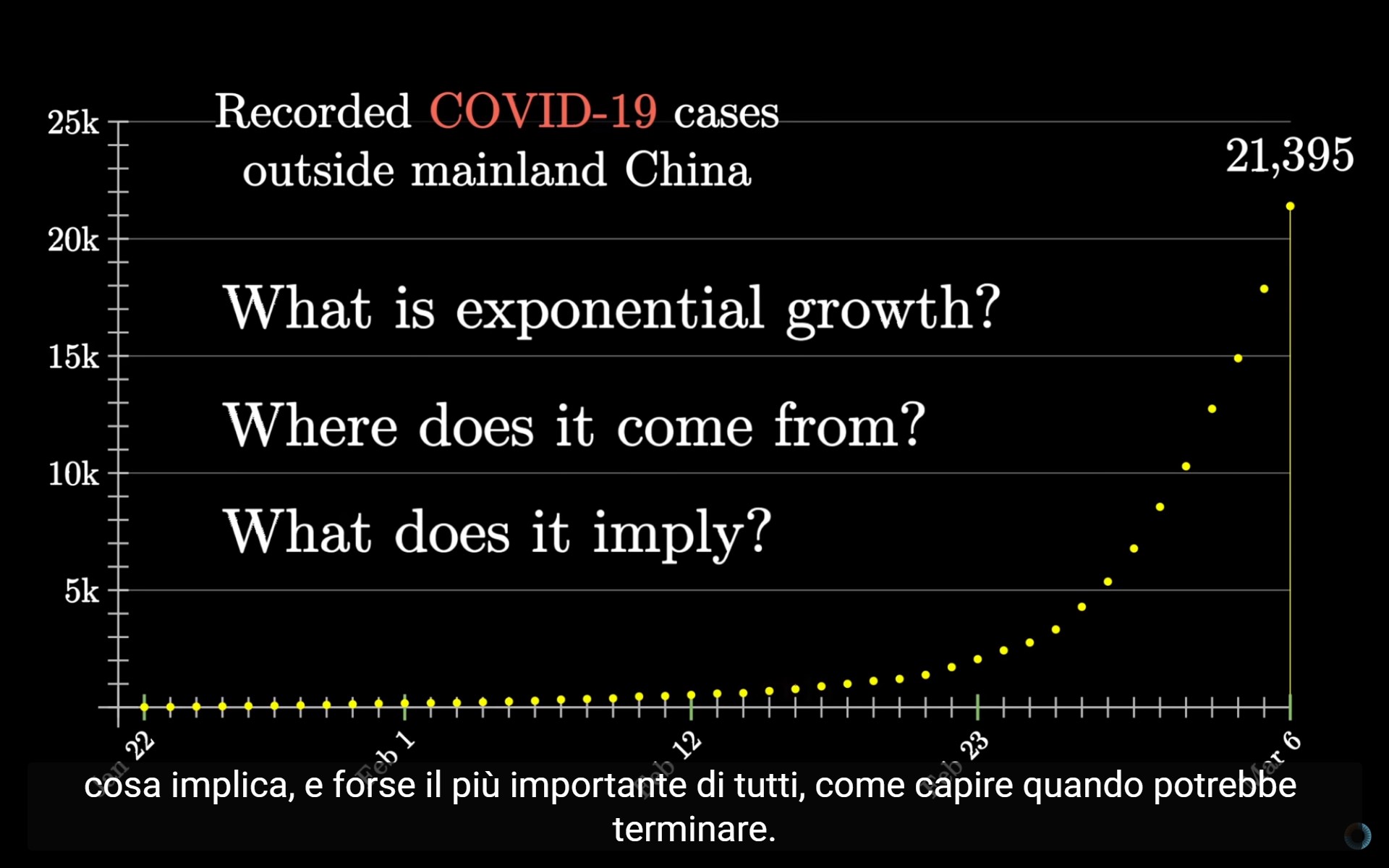
Di seguito prenderemo come dati di esempio i casi di COVID-19 registrati fuori dalla Cina.
L’aumento di casi rispetto al giorno precedente (ΔNd) sarà pari al prodotto di tre fattori:
- il numero di casi in un determinato giorno (Nd)
- il numero medio di persone che un infetto incontra ogni giorno (E)
- la probabilità che ogni esposizione, cioè di contatto tra individuo infetto e individuo suscettibile di ammalarsi, diventi un’infezione (p)

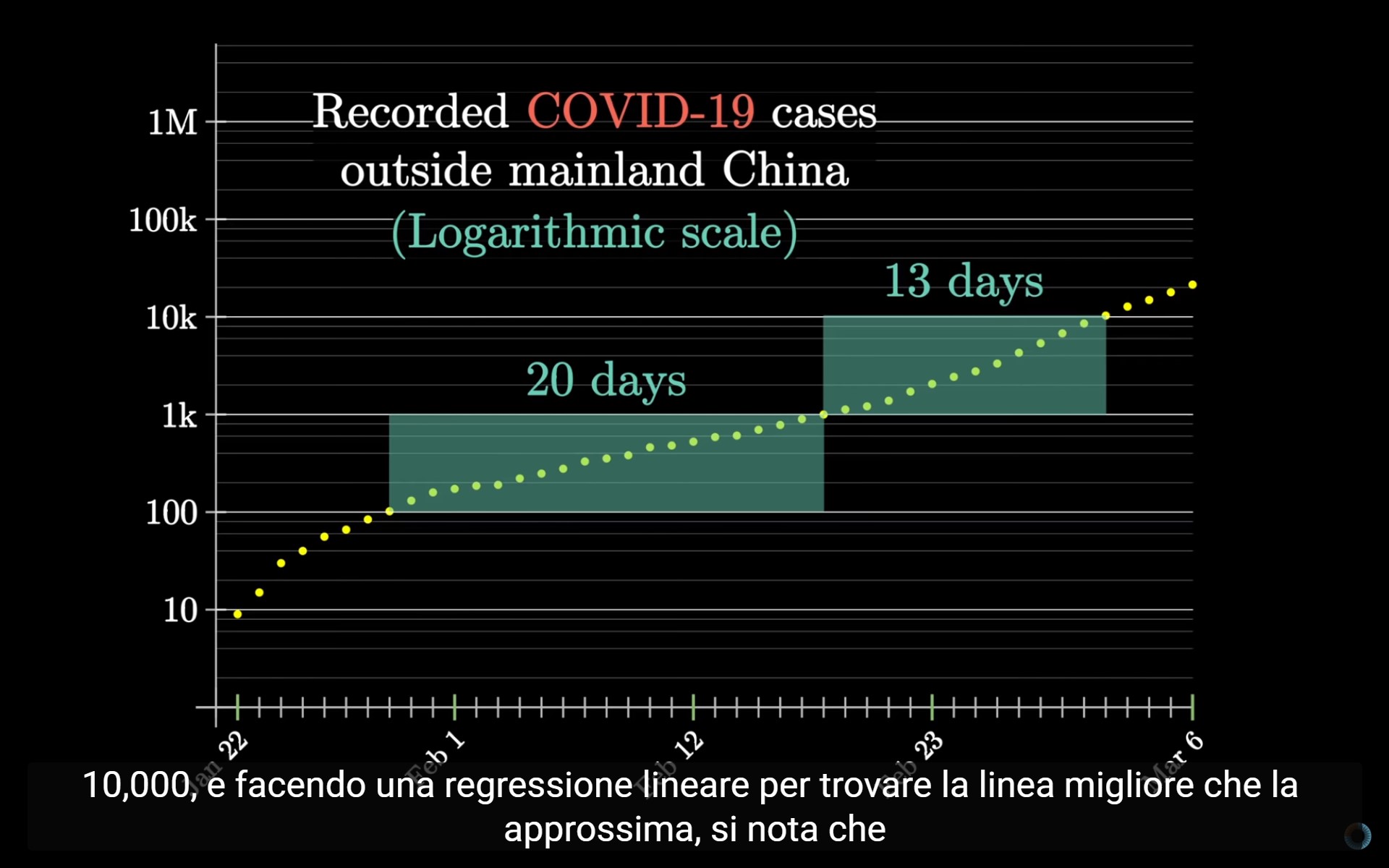
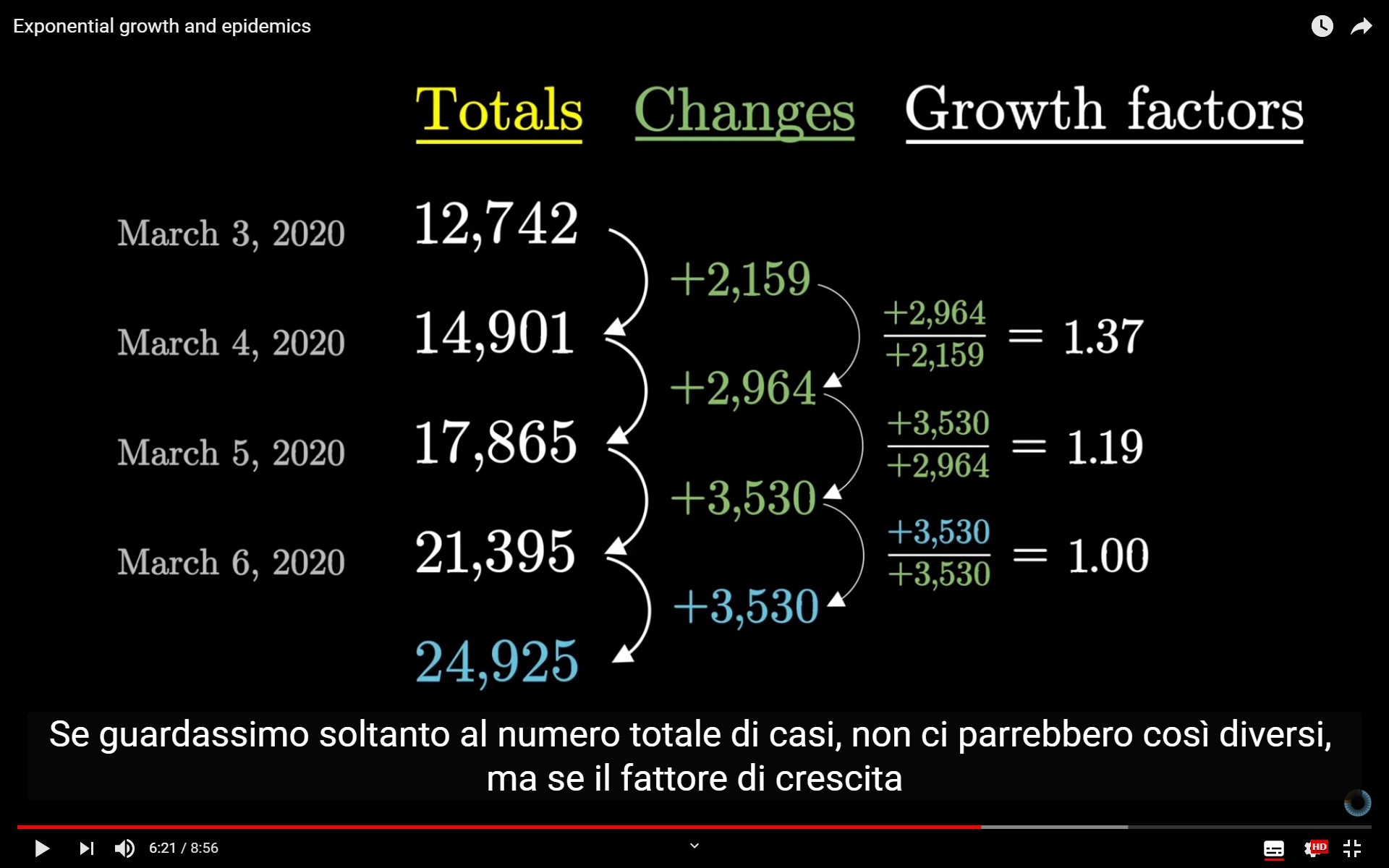
Basandoci sui numeri, sono serviti 20 giorni per passare da 100 a 1000 casi, e quindi 13 giorni passare da 1.000 a 10.000.
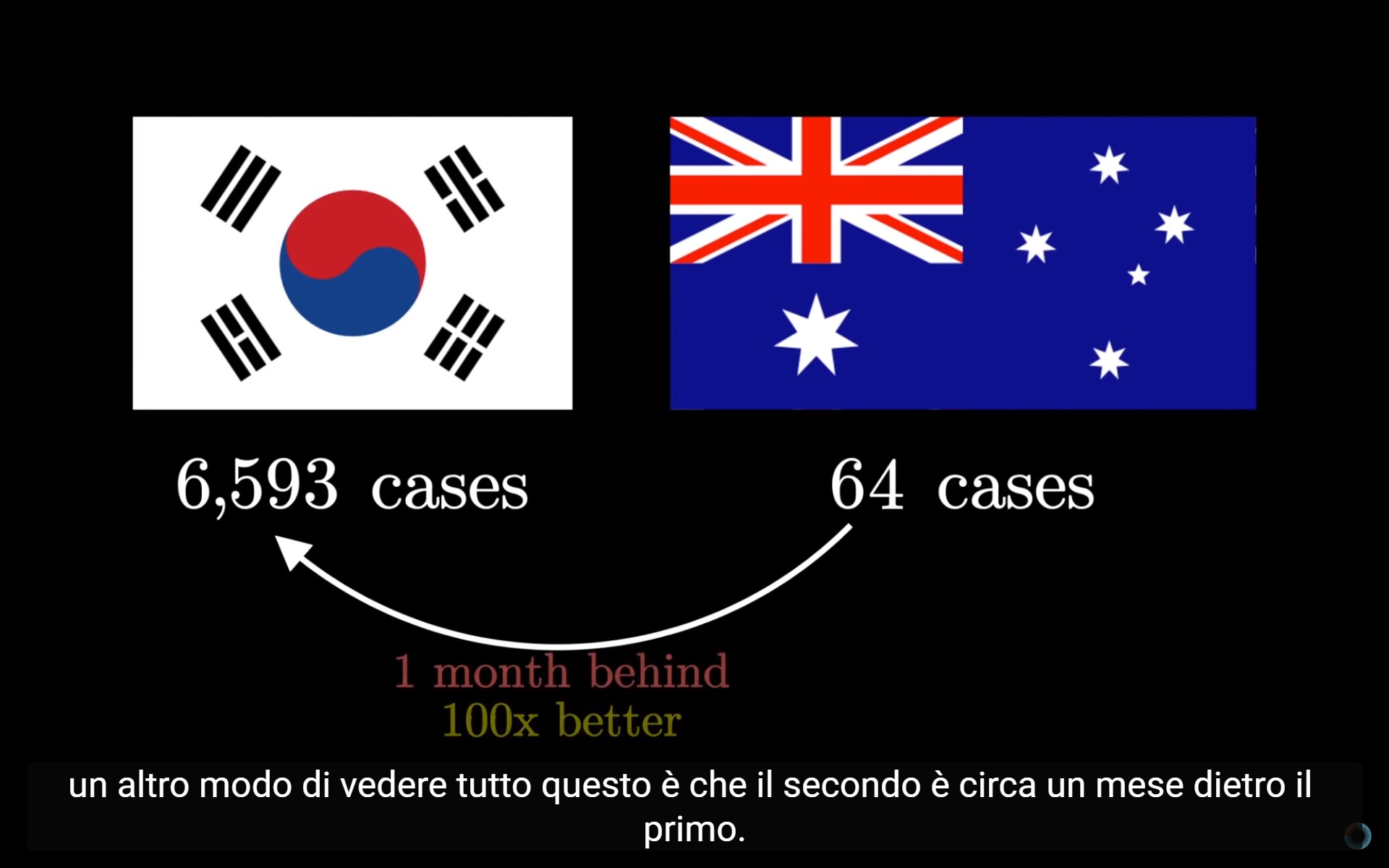
Se vediamo che un paese ha un decimo dei casi di un altro paese, è facile pensare che questo se la passi meglio. Ma se ci rendiamo conto che il tasso di crescita del fenomeno è comune, allora la prospettiva cambia: semplicemente, il secondo paese è temporalmente un mese indietro al primo nella diffusione del virus.
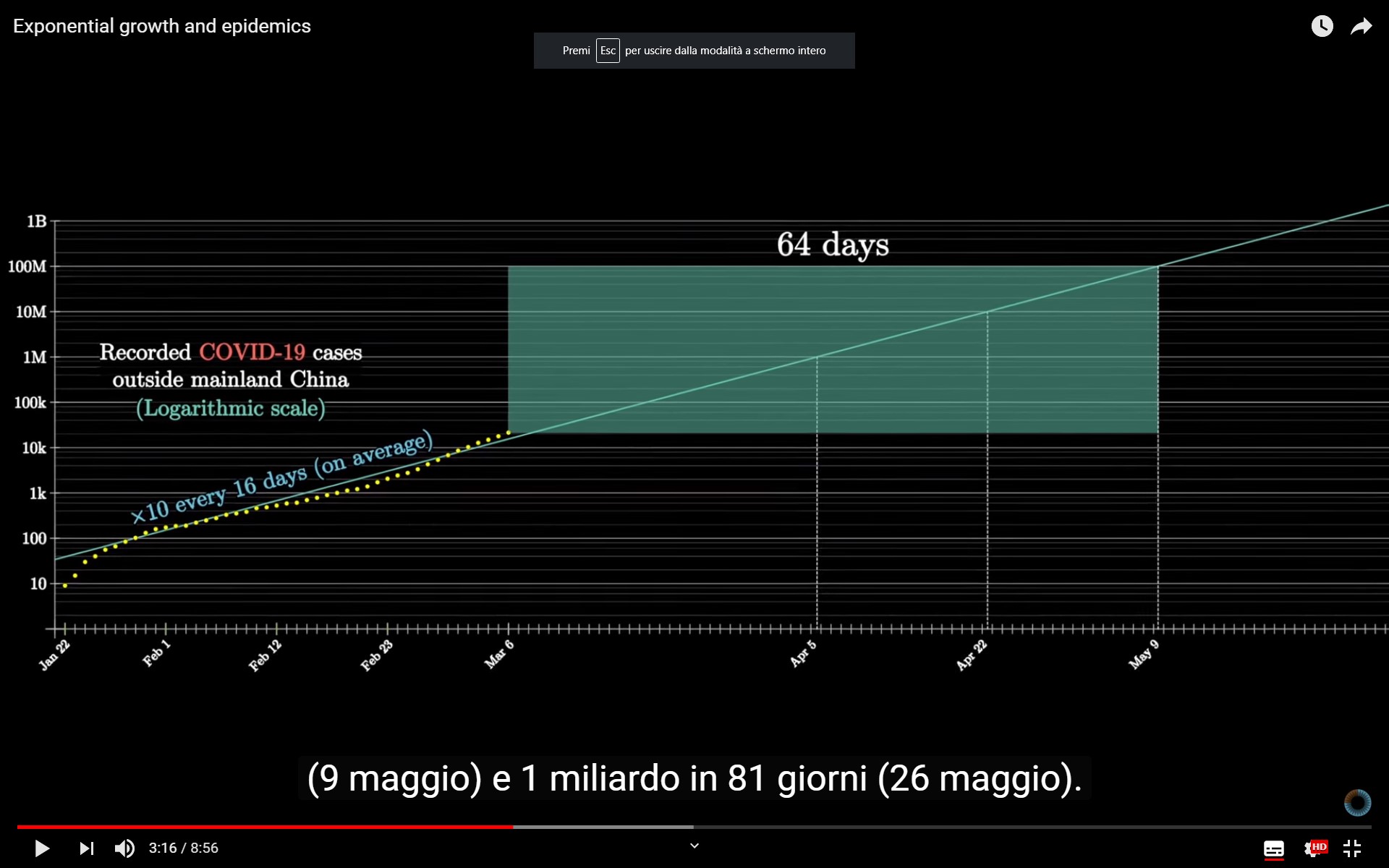
Se l’andamento attuale continuasse con la stessa tendenza, questo significa che ci sarebbero:
- 1 milione di casi il 5 aprile,
- 10 milioni il 22 aprile,
- 100 milioni il 9 maggio,
- 1 miliardo il 26 maggio.
Dato che la crescita non potrà essere all’infinito, la domanda cruciale per tutte le epidemie è: quando la curva inizierà a cambiare pendenza?
Tornando alla formula precedentemente descritta, l’unico è modo e far sì che:
- E –> il numero medio di persone che un infetto incontra ogni giorno
oppure
- p –> la probabilità che ogni esposizione (cioè il contatto tra individuo infetto e individuo suscettibile di ammalarsi) diventi un’infezione
ad un certo punto decrescano.

E questo è inevitabile accada: anche nello scenario peggiore, ad un certo punto la maggior parte delle persone esposte al virus sarà già infetta e tali persone non potranno quindi trasformarsi in nuovi casi.

I veri modelli esponenziali non esistono nel mondo reale, ma all’inizio sono solo identici a delle curve logistiche.
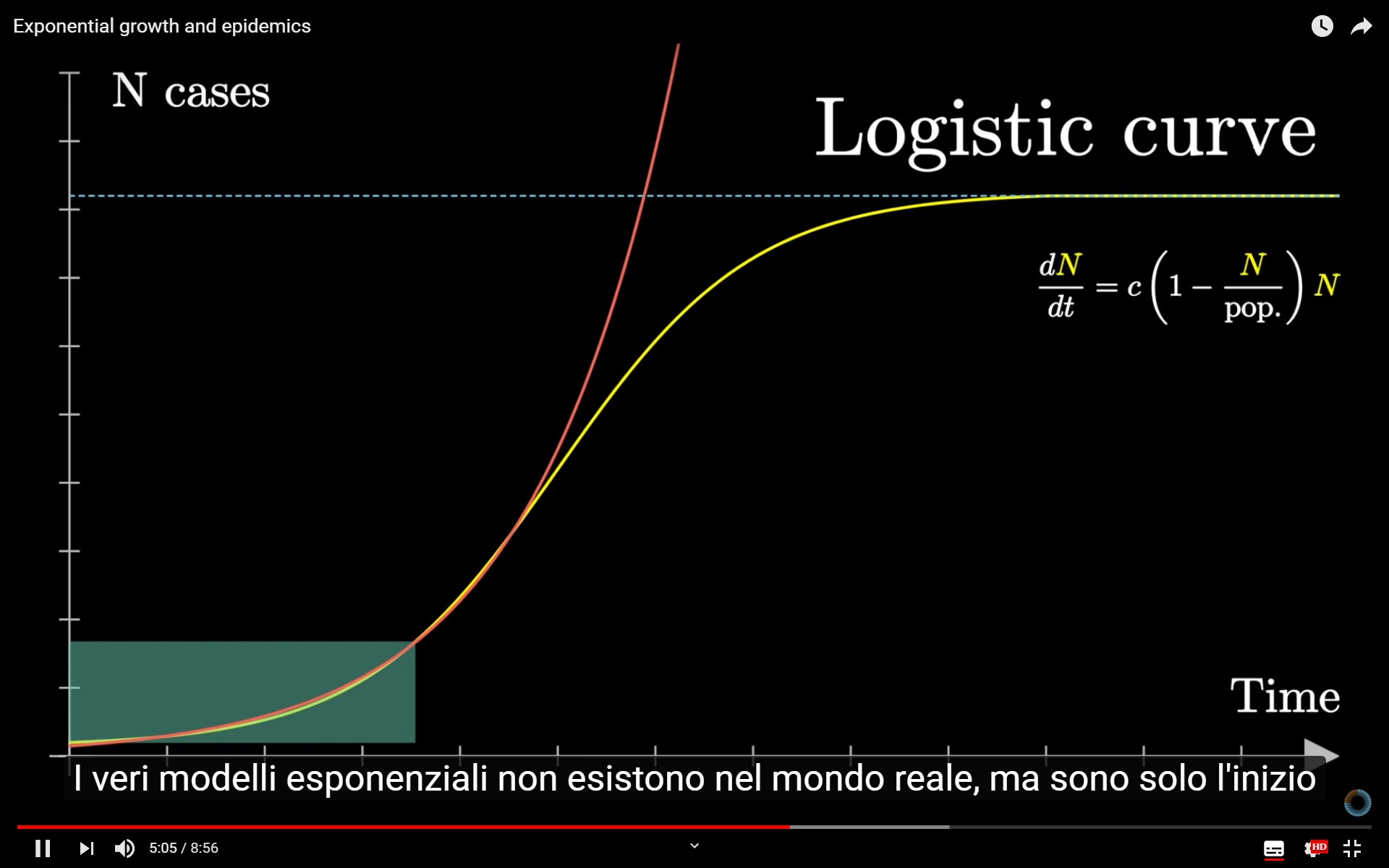
Il punto in cui la curva passa da una inclinazione positiva verso l’alto ad una negativa verso il basso, è noto come “punto di flesso” (inflection point).
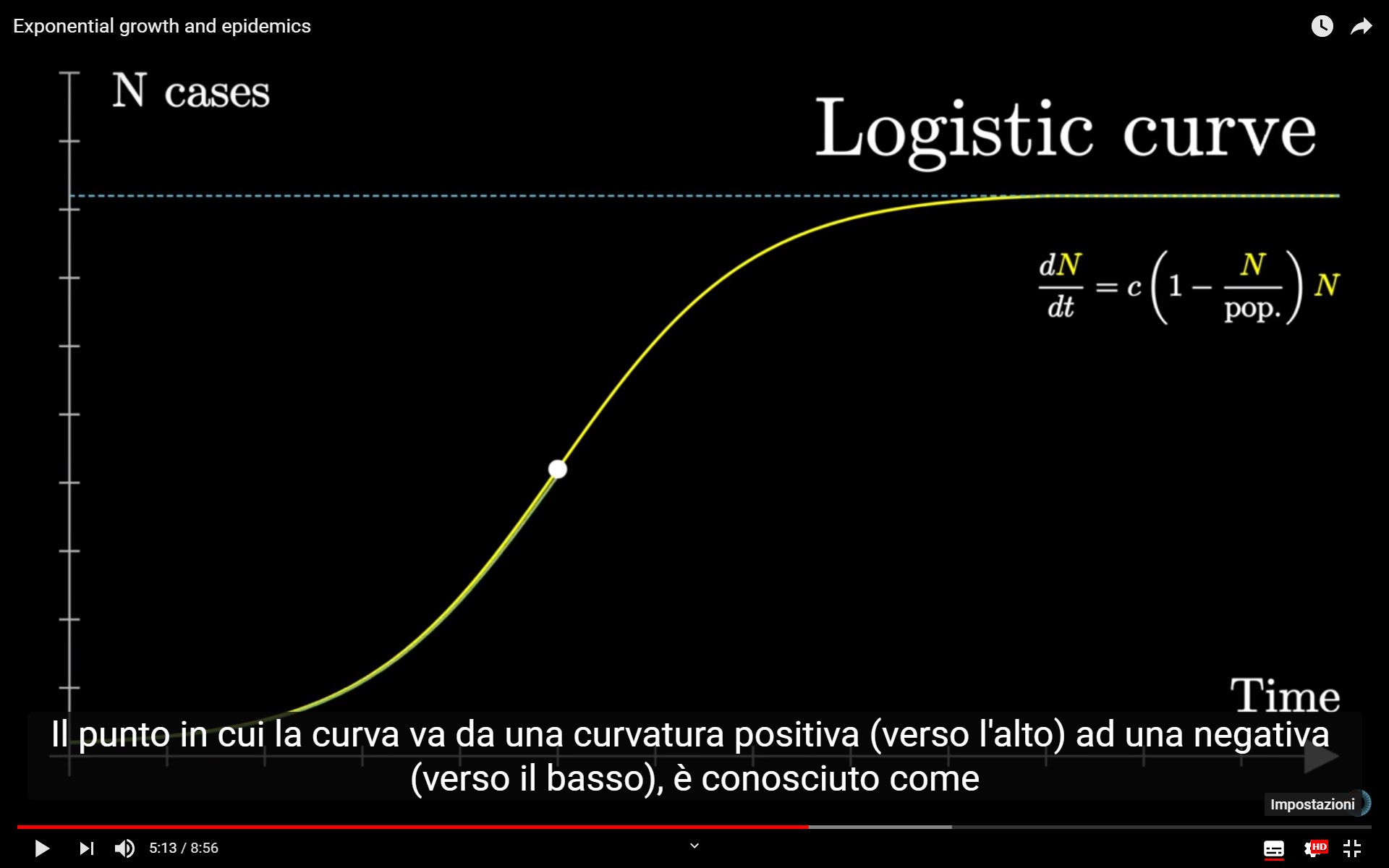
Superato quel punto, il numero di nuovi casi ogni giorno diventa più o meno costante, e comincia quindi a diminuire.

Durante un’epidemia spesso ci si concentra sul tasso di crescita (growth factor), che indica il rapporto tra nuovi casi di un determinato giorno e il numero di nuovi casi del giorno precedente.

Il fattore di crescita è quindi il rapporto tra due cambiamenti successivi (cioè ad esempio dei nuovi casi del 4 marzo messi in relazione ai nuovi casi del 3 marzo).

Quando siamo nella parte esponenziale della curva (cioè all’inizio dell’epidemia), il fattore di crescita sarà sempre maggiore di 1 (nell’immagine qui sotto è pari a 1.06).
Fino a quando, ad un certo punto, il fattore arriverà ad essere pari a 1 nel punto di flesso (inflection point).
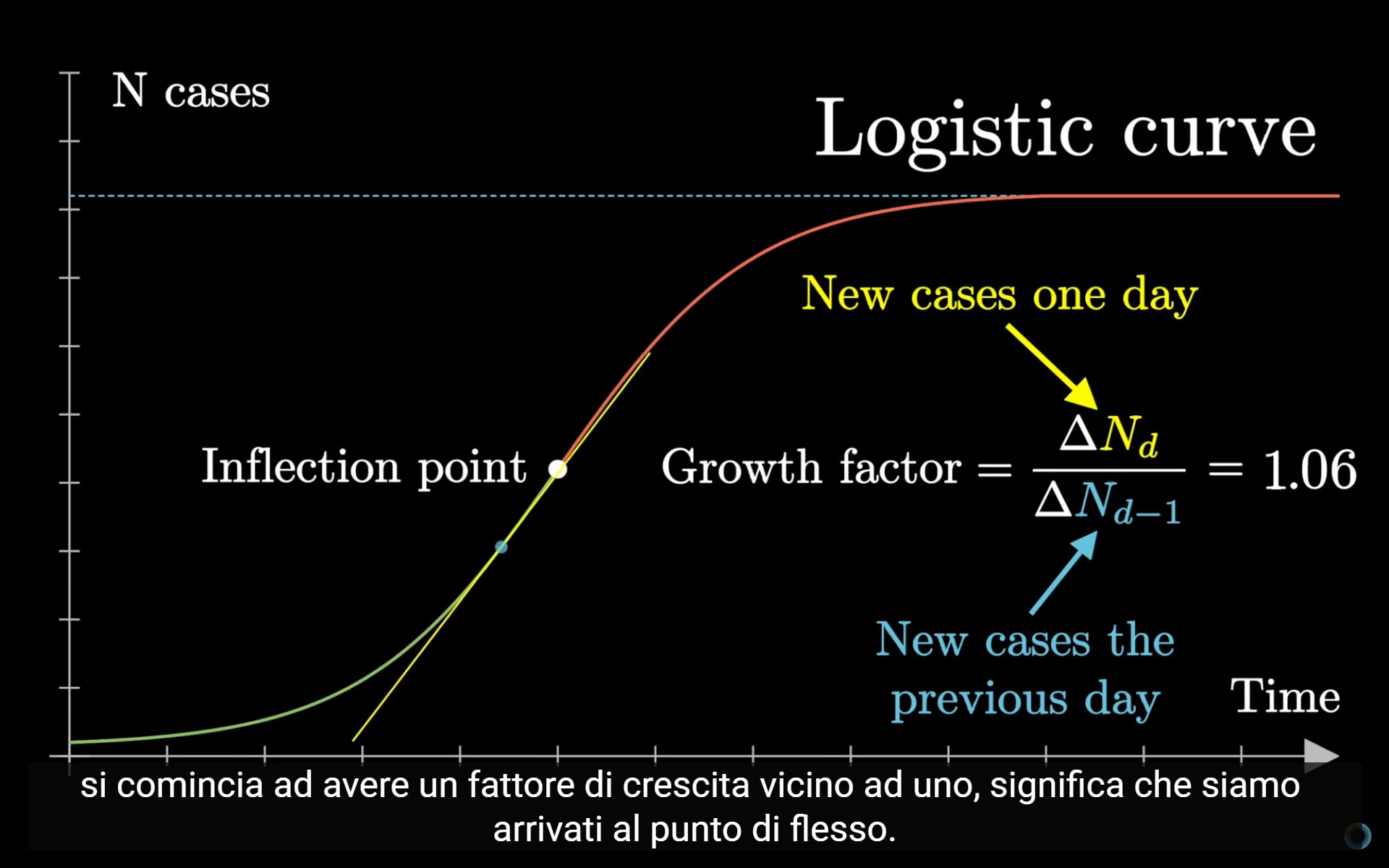
Immaginiamo, ad esempio, se il 7 marzo il numero di nuovi casi fosse uguale (+3530) al numero di nuovi casi del 6 marzo. Apparentemente non sembrerebbe così positivo. Ma come possiamo vedere in basso a destra, significherebbe che il tasso di crescita è pari a 1. Cioè al punto di flesso.
Se, nel caso peggiore, questo punto di saturazione fosse pari al totale della popolazione

è ovvio che le persone sono sparse nel mondo in maniera casuale; ma sono raggruppate in comunità, che però purtroppo comunicano tra loro attraverso gli spostamenti degli individui (infetti).

Fortunatamente, far ammalare tutta la popolazione non è l’unico modo di rallentare il tasso di crescita del virus, che può diminuire:
- se le persone smettono di incontrarsi e viaggiare –> si abbassa E, cioè il numero medio di persone che un infetto incontra ogni giorno;

- se le persone iniziano a lavarsi di più le mani –> si abbassa p, la probabilità di esposizione ad un’infezione.

Un aspetto che può farci essere ottimisti è che la crescita esponenziale è estremamente sensibile a questa costante.
Come potete vedere sulla parte destra del video, se il tasso di crescita giornaliero è del 15% (cioè 1.15) rispetto a 21.000 casi, significa che in 61 giorni i nuovi infetti saranno oltre 105 milioni.
Ma se invece il tasso fosse solamente del 5% (cioè 1.05, sempre riportato sulla destra del video), i nuovi casi di infetti, dopo 61 giorni, sarebbero “soltanto” 411 mila.

Quindi: se le persone sono poco preoccupate (e quindi continuano a viaggiare e a non lavarsi le mani), c’è da preoccuparsi; se le persone sono abbastanza preoccupate, possiamo stare tranquilli.
Così come riportato nella chiusura del video: “the only thing to fear is the lack of fear itself”. L’unica paura da avere è l’assenza di paura.
