Nel quinto web meeting della serie Complessità in azione: otto leve per cambiare il mondo, si è parlato di complessità in relazione all’impatto del digitale sulla vita sociale, ospiti Alessandro Vespignani e Barbara Carfagna.
Qui il video della rubrica “Agopunture digitali” di Massimo Conte; di seguito l’articolo con i riferimenti citati, per chi vuole approfondire.
Clicca qui per vedere tutte le puntate di “Agopunture digitali”
Il tema di questa puntata di Agopunture Digitali è legato alla diffusione dell’innovazione attraverso le reti sociali.
Per parlarne, ci avvaliamo dell’articolo interattivo Going Critical, realizzato da Kevin Simler.
Come si propaga l’innovazione? Le soglie critiche nelle reti possono venire in nostro aiuto.
1.
Se vogliamo studiare la diffusione di un fenomeno, partiamo da una rete in cui ci sono nodi e connessioni. Alcuni nodi sono attivi (o infetti). Quindi un fenomeno (ad esempio un’infezione, o anche una pratica culturale) può propagarsi attraverso la rete.
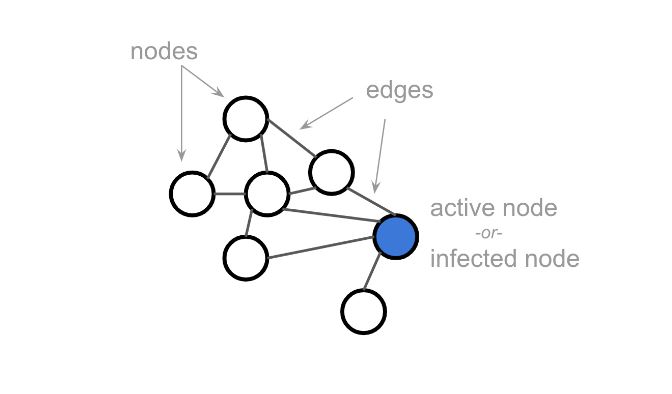
La stessa rete può essere rappresentata come reticolo. Il nodo al centro in blu è sempre quello attivo già mostrato sopra.
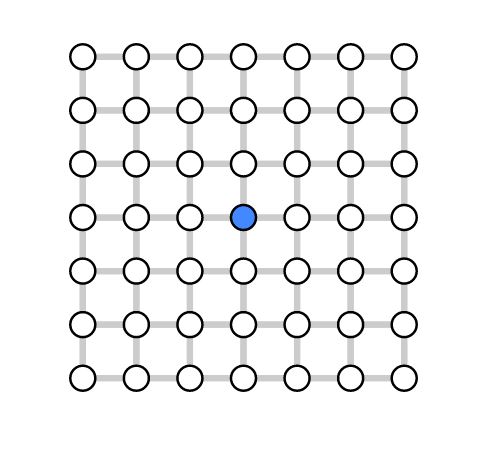
Come possiamo vedere, in questo tipo di reticoli ogni nodo ha quattro vicini: sopra, sotto, a destra, a sinistra. Lo stesso reticolo, per semplificazione grafica e proseguire poi con la nostra simulazione, da qui in avanti sarà rappresentato da quadratini. Ogni quadratino è un nodo, che confina e comunica con altri quattro nodi.
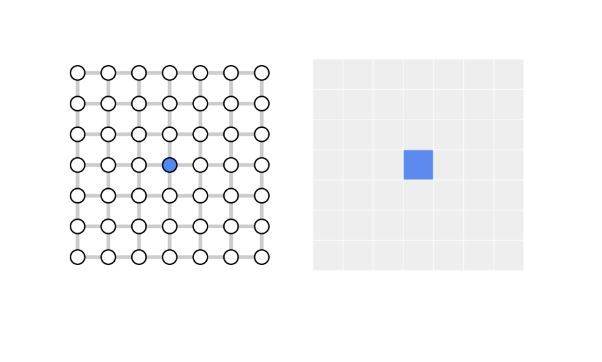
2.
Ragioniamo su un modello probabilistico: a partire dal nodo centrale blu, inizialmente attivo, quale probabilità c’è che i nodi vicini si attivino?
Nota importante: da questo punto in poi le immagini mostrano uno stato dei simulatori dell’articolo originale in inglese, in cui si possono fare delle prove in prima persona. Quindi: se preferisci leggere in italiano una sintesi, continua qui.
Se sei a tuo agio con l’inglese, passa direttamente all’articolo Going critical.
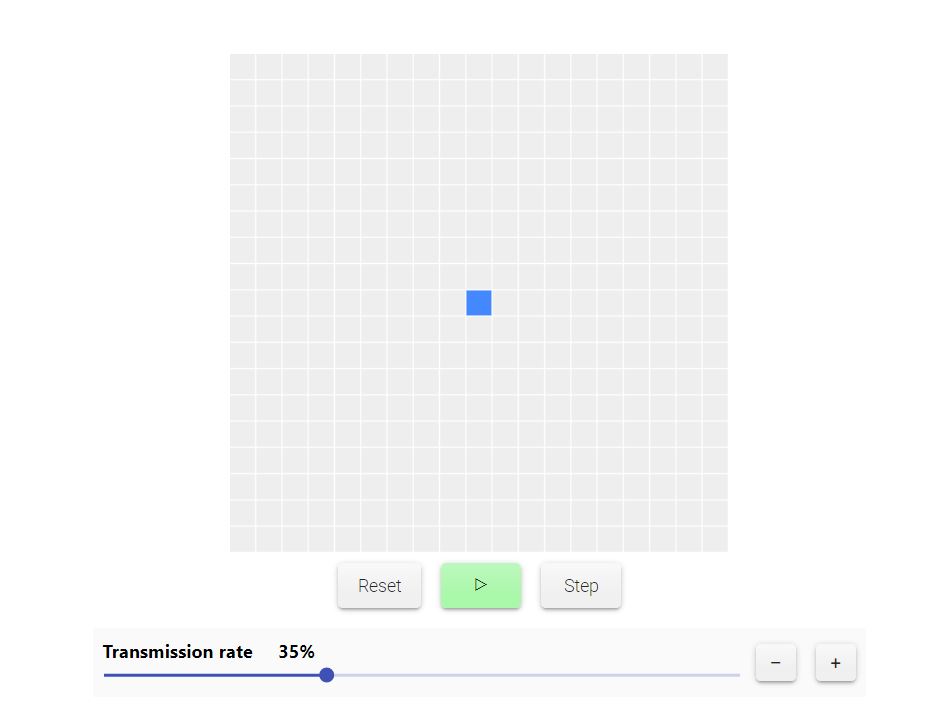
Abbiamo sotto ogni griglia un cursore, che ci consente di regolare il tasso di trasmissione all’interno della rete.
In questo caso il modello alla base della simulazione e della rappresentazioen grafica è SIS, cioè Susceptible–Infected–Susceptible. Facciamo un esempio, anziché con un’epidemia, con una trasmissione di pratiche culturali:
- Suscettibile, perché il nodo non ha mai fatto quella cosa, non è attivo ma potrebbe diventarlo;
- Infetto/ATTIVO, perché magari il nodo/soggetto adotta un determinato comportamento o pratica;
- Suscettibile, può tornare nello stato suscettibile quando smette di fare quel determinato atto.
3.
In un modello SIS, poiché i nodi (a differenza del modello SIR, che vedremo più avanti) non diventano mai Removed (nel caso di un’infezione è se l’elemento è immunizzato oppure è deceduto, cioè rimosso dal numero dei potenziali soggetti Suscettivili), una rete relativamente piccola può tenere in vita il fenomeno di diffusione per molto tempo.
In questo esempio che stiamo portando avanti, sotto il 30% l’infezione si spegne dopo poco. Sopra il 30% continua a autoalimentarsi, c’è una soglia critica.
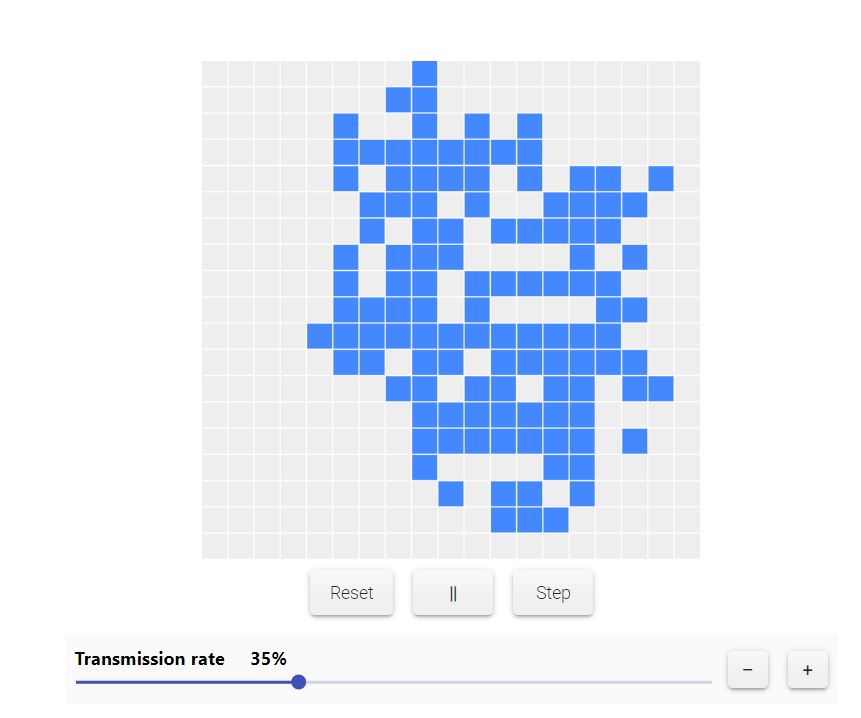
4.
Nelle reti complesse possono esserci dei precisi tipping point (punti di non ritorno) che separano le reti sottosoglia (in cui il fenomeno è destinato ad estinguersi) dalle reti supercritiche, in cui il fenomeno si mantiene in vita con una crescita senza fine.
Questo punto di svolta è chiamato soglia critica, è una caratteristica generale dei processi di diffusione di reti regolari. Il valore preciso di questa soglia varia da rete a rete.
In questa nostra rete, ad esempio, è tra il 22 e il 23% del tasso di trasmissione. Sotto il 22% il fenomeno non è in grado di propagarsi (per chi vuole approfondire: percolation threshold, soglia di percolazione).
Sotto la soglia critica, siamo sicuri che il fenomeno/infezione si estinguerà; ma se siamo su valori intorno alla soglia critica, è possibile che il fenomeno continui a propagarsi e autoriprodursi; anche se non è sicuro che si riproduca per sempre.
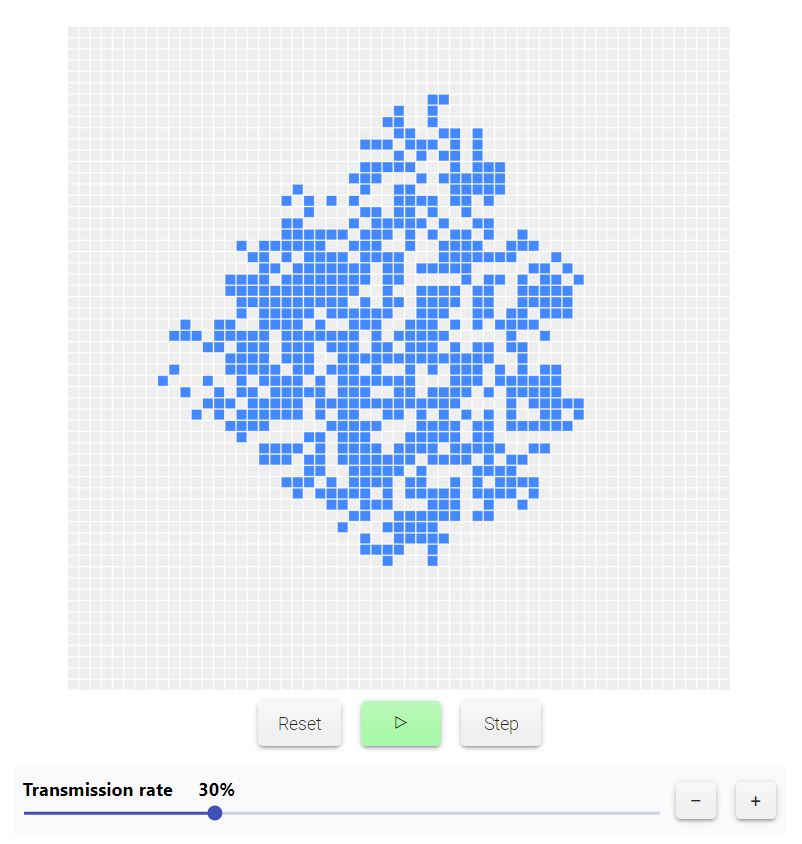
5.
Ci potrebbe essere anche parametro di attivazione spontanea, cioè nodi che si attivano senza essere contagiati da nodi vicini. Ma non è quello che influenza la dinamica in modo determinante, resta il tasso di trasmissione che determina se una rete è subcritica o supercritica.
È come cercare di appiccare un incendio in un campo bagnato o in uno secco: nel primo caso, dei piccoli fuochi locali si spegneranno, senza possibilità di propagazione (è cioè sotto soglia). Se è una rete supercritica, cioè un campo molto secco, basterà poco per scatenare un incendio.
Lo stesso succede per idee e invenzioni. Se il mondo non è pronto per un’idea, piccoli fuochi locali non continueranno a propagarsi, non avrà cioè successo. Ci sono idee (come l’agricoltura e la scrittura) inventate più volte in più luoghi nel corso della storia umana, ma che non si sono diffuse in tutta la rete, poiché probabilmente il tasso di diffusione di quel fenomeno non era abbastanza forte.
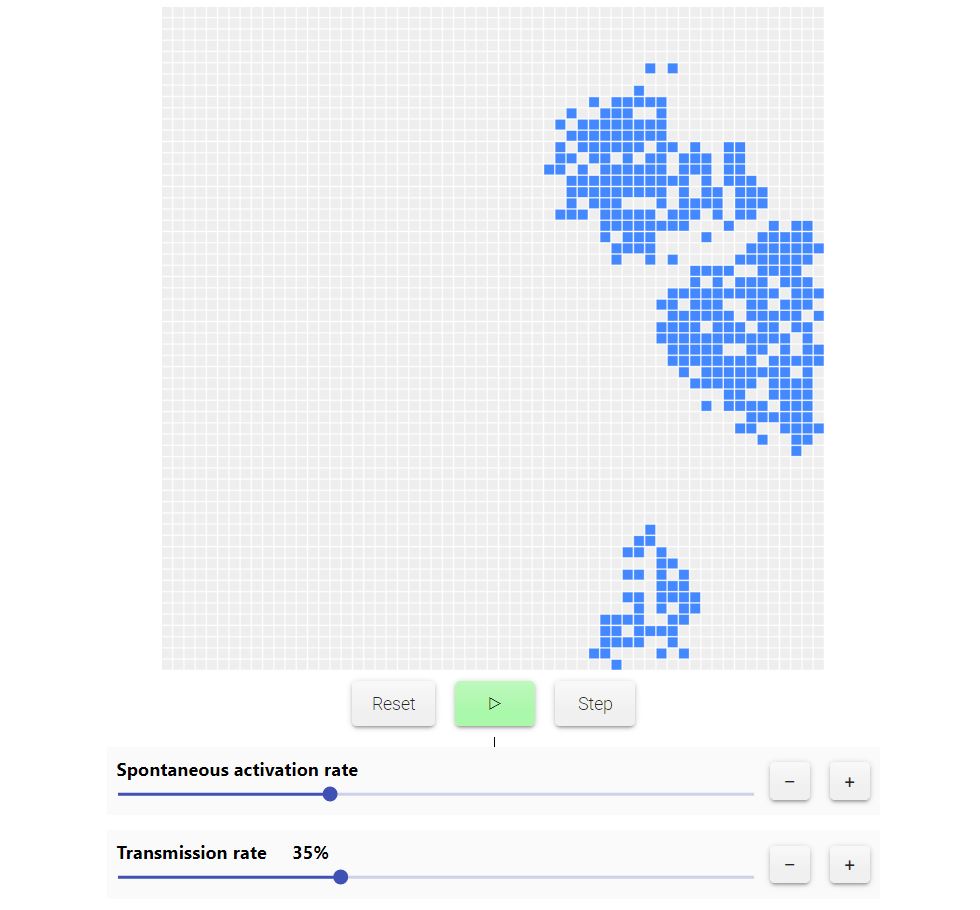
6.
Vediamo un ultimo passaggio sull’immunità in un modello leggermente diverso, il SIR, in cui la R indica che ci sono elementi in stato Removed, che non possono essere infettati. A seconda di come varia questo parametro, l’infezione si propagherà o no.
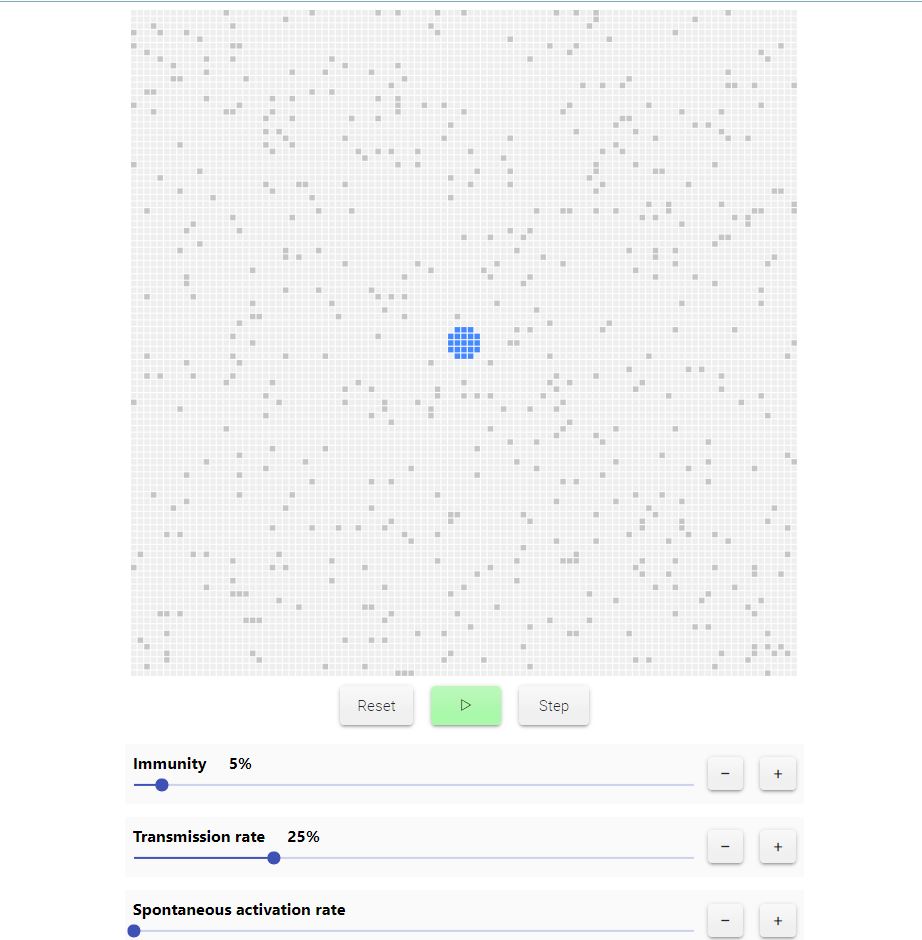
Il tasso di immunità determina se la rete è subcritica o supercritica. Ad esempio questo spiega il motivo per cui nelle aree boschive vengono lasciati degli spazi vuoti: esattamente per evitare che un eventuale incendio locale diventi globale.
Punto di arrivo di questa puntata: la scienza delle reti può aiutarci a comprendere la propagazione di fenomeni all’interno di sistemi; per influenzare questa diffusione (o meno) possiamo agire su alcuni parametri legati sia alle caratteristiche dei singoli (stato susceptible / infected / removed) sia su alcune caratteristiche delle connessioni, cioè di sistema.
Questa generalizzazione poi va declinata per ogni peculiare sistema complesso; ragionare sulle soglie critiche ci consente di capire come piccoli cambiamenti locali in un sistema complesso possano generare effetti più ampi e globali.
